Логика Порецкого
Аннотация
Прослежена история создания логики в России. Отмечен приоритет России как в области решения логических уравнений, так и в аналитическом представлении силлогистических общеутвердительных и общеотрицательных функторов. Доказано,что аналитические методы решения логических уравнений, разработанные более 100 лет назад Порецким П.С., применялись им также для синтеза силлогизмов(соритов). Показано, что способы Порецкого вполне пригодны для синтеза любых силлогизмов с общеутвердительным или общеотрицательным заключением.
Платон Сергеевич Порецкий родился 3 октября 1846 г. в Елизаветграде Херсонской губернии в семье военного врача[1]. В 1870 г. закончил физматфак Харьковского университета. Был оставлен прфессорским стипендиатом на кафедре астрономии. С 1876 г. избирается астрономом-наблюдателем Казанского университета. За 1876-79 гг. Порецкий опубликовал 2 тома наблюдений на меридианном круге. Несмотря на слабое здоровье участвует в общественной жизни университета, являясь секретарем секции физматнаук, казначеем, а затем и пожизненным членом. Редактирует либеральную газету "Телеграф".
За астрономические исследования в 1886 г. ему присуждается ученая степень доктора астрономии и звание приват-доцента.
Принимал заочное участие в ряде международных научных конгрессов, вел активную переписку как с русскими, так и иностранными учеными.
П.С.Порецкий умер 9 августа 1907 г. в с.Жоведь Гродненского уезда Черниговской губернии, куда переехал из Казани в 1889 г., будучи уже тяжелобольным. Смерть застала его за неоконченной статьей по логике.
Логикой занимается с 1880 г. В 1881 г. выходит его работа "Изложение основных начал мат.логики ...". В 1881 г. издает свой большой труд "О способах решения логических равенств и об обратном способе математической логики"[2], где излагает теорию логических равенств, закон форм посылок, закон замещения системы посылок одной посылкою, закон разложения посылок на элементы, закон исключения терминов из посылок, закон умозаключений(синтез), закон причин. Порецкий далёк от претензии построить универсальное логическое исчисление. В предисловии к [2] он чётко заявляет, что развиваемое им исчисление пригодно лишь для "качественных" умозаключений("качество" в понимании Порецкого соответствует одноместному предикату). В логических равенствах Порецкий использует суждения только общего характера(утвердительные или отрицательные). Более того, можно утверждать, что в случае получения частного заключения эти методы не работают. Решение подобных задач изложено в [3].
Работа П.С.Порецкого "Из области математической логики"(1902) является обобщением классической силлогистики. Синтезируется несколько заключений из заданных посылок(элиминация), что даёт возможность доказать отсутствие каких-либо других следствий, помимо следствий искомого вида. Элиминацию до сих пор не освоила современная логика.
Попытаемся с современных позиций проанализировать достижения и неудачи великого русского логика в области решения логических равенств. Под решением логического уравнения будем понимать преобразование исходного уравнения к явному виду относительно одной из переменных. При решении системы логических уравнений вначале определяется так называемая полная единица задачи (системы), а потом отыскивается решение уравнения относительно заданных переменных. Решение логического уравнения осуществляется в соответствии с алгоритмом "Селигер"[4].
Алгоритм "Селигер"
Пример 1
Рассмотрим 1-ю задачу Порецкого[2]. Между птицами данного зоосада существуют 5 отношений:
Определить, были ли птицы качества X певчие или нет. Узнать то же в отношении птиц качества Y. Найти, были ли среди птиц качества X птицы качества Y и наоборот.
Решение
Прежде всего необходимо отметить,что все 5 отношений являются по существу общеутвердительными и общеотрицательными посылками сорита,т.е.фактически речь идет о синтезе заключения в сорите.
Пусть X - птицы качества X,
Y - птицы качества Y,
S - певчие птицы,
G - крупные птицы.
Тогда условие задачи будет представлено следующими рекурсивными уравнениями[2](здесь и далее апостроф обозначает отрицание):
Уравнения Порецкий через эквивалентность приводит к единичной форме:
Основываясь на введенном нами русском базисе силлогистики[3] Axy = x'+y и Exy = x'+y', созданном при помощи скалярных диаграмм, можно получить эти же соотношения более простым путем :
Однако восхищает красота решения задачи П.С.Порецким без привлечения современной математической логики. Фактически русский ученый впервые в мире вывел соотношения для силлогистических функторов Аху и Еху в виде:
Axy = (x = xy), Exy = (x = xy').
После раскрытия скобок по формуле эквивалентности мы получим формулы русского базиса[3]. Современная силлогистика до сих пор не замечает и не использует этих результатов великого русского логика. Кроме того, данная система уравнений представляет из себя 5 посылок силлогизма, точнее сорита.Таким образом, решив систему уравнений,Порецкий впервые в мире синтезировал аналитически заключение силлогизма(сорита).
Полная логическая единица всей задачи определяется Порецким как конъюнкция всех левых частей системы логических уравнений .Эту рутинную операцию можно заменить на менее утомительную процедуру построения дизъюнкции нулей.Получим систему[4]:
Полный логический нуль системы равен дизъюнкции всех левых частей системы логических уравнений .Проведем решение задачи Порецкого с использованием карты Карно.Заполним карту Карно нулями в соответствии с нулевыми термами системы,а в оставшиеся клетки впишем единицы. Тогда минимальная дизъюнктивная нормальная форма (МДНФ) полной логической единицы всей задачи примет вид:
M=sy+gx'
xy
\ 00 01 11 10
gs \------------------+
00¦ 0 ¦ 0 ¦ 0 ¦ 0 ¦
+----+----+----+---+
01¦ 0 ¦ 1 ¦ 1 ¦ 0 ¦
+----+----+----+---+
11¦ 1 ¦ 1 ¦ 1 ¦ 0 ¦
+----+----+----+---+
10¦ 1 ¦ 1 ¦ 0 ¦ 0 ¦
+------------------+
Рис.1
Выпишем из карты Карно все единичные термы в виде таблицы истинности (табл.1). По табл.1 построим табл.2 для x = f1(g,s),табл.3 для y = f2(g,s) и табл.4 для y = f3(x). Если на каком-либо наборе функция принимает значение как 0, так и 1, то в соответствующую клетку карты Карно вписываем i. Если какой-либо набор отсутствует, то для этого набора в карту Карно вносим значение j при четырехзначной логике[4]. Карты Карно для табл.2,3 и 4 представлены на рис.2,3 и 4 соответственно.
Табл.1 Табл.2 Табл.3 Табл.4
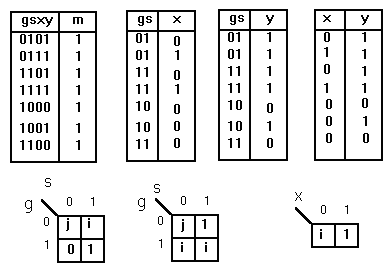
Рис.2 Рис.3 Рис.4
После минимизации получим для четырехзначной логики систему уравнений[4] :
x = is + jg's' y = g's + ig + jg's' y = x + ix' = (x + ix) + ix' = x + i
Результаты,полученные Порецким :
x = xs y = g's + gy y = y + x
Результаты Порецкого менее корректны,поскольку он использует 2-значную(с некоторой натяжкой ее можно считать псевдо-трехзначной: здесь в качестве i выступает символ функции,встречающийся в правой части уравнений) логику вместо 4-значной. Метод Порецкого корректен при общих посылках и общем заключении, но он абсолютно непригоден для частных посылок и частных заключений. Порецкий своими методами мог бы частично обосновать русскую силлогистику[3], в том числе доказать некорректность 1-го модуса 4-й фигуры.
Аксиоматика Порецкого
В [1] утверждается, что аксиоматика Порецкого имеет вид:
1) a -> a, 2) ((a -> b)(b -> c)) -> (a -> c), 3) (ab) -> a, 4) (ab) -> b, 5) ((a -> b)(a -> c)) -> (a -> (bc)), 6) ((a -> b)(b -> a)) -> (a = b), 7) (a = b) -> (a -> b), 8) (a = b) -> (b -> a).
Непонятно, почему все эти соотношения называются аксиомами, поскольку они легко и просто доказываются с помощью алгоритма "Импульс"[5].
Алгоритм "Импульс"
Алгоритм анализа законов логики суждений чрезвычайно прост :
Воспользуемся алгоритмом "Импульс" для доказательства того, что все аксиомы Порецкого являются теоремами:
1) a -> a = a' + a = 1, 2) ((a -> b)(b -> c)) -> (a -> c) = ((a'+b)(b'+c)) -> (a'+c) = ab'+bc'+a'+c = 1, 3) (ab) -> a = a'+b'+a = 1, 4) (ab) -> b = a'+b'+b = 1, 5) ((a -> b)(a -> c)) -> (a -> (bc)) = ((a'+b)(a'+c)) -> (a'+bc) = ab'+ac'+a'+bc = 1, 6) ((a -> b)(b -> a)) -> (a = b) = ((a'+b)(b'+a)) -> (a=b) = ab'+ba'+ab+a'b' = 1, 7) (a = b) -> (a -> b) = ab'+ba'+a'+b = 1, 8) (a = b) -> (b -> a) = ab'+ba'+b'+a = 1.
Стяжкин Н.И.[1] приводит исчисление Порецкого в виде длинного списка из более чем 20 аксиом и правил:
(1A) e = e - принцип тождества; (2П) (e=c) -> (c=e) - симметричность равенства; (3П) ((e=c)&(c=b)) -> (e=b) - транзитивность равенства; (4A) ee = e - идемпотентность умножения; (4*A) e+e = e - идемпотентность сложения; (5A) ec = ce - коммутативность умножения; (5*A) e+c = c+e - коммутативность сложения; (6A) (ec)b = e(cb) - ассоциативность умножения; (6*A) (e+c)+b = e+(c+b) - ассоциативность сложения; (7A) e(e+c) = e - принцип поглощения; (7*A) e+ec = e - принцип поглощения; (9П) (e=c) -> (e+b=c+b); (9*П) (e=c) -> (eb=cb); (10A) e(c+b) = ec+eb; (11A) e+e' = 1; (11*A) e&e' = 0; (12A) e&0 = 0; (12*A) e&1 = e.
Нет нужды доказывать, что весь этот набор аксиом и правил на самом деле является набором теорем, которые легко выводятся по алгоритму "Импульс". Более того, на стр.377 [1] долго и многословно поясняется, как с помощью аксиом и правил можно доказать одну из теорем логических следствий Порецкого. Покажем, как просто это делается по алгоритму "Импульс"(здесь переменная e1 заменена на c):
(e=ec) -> (e=e(c+x)) = e(ec)'+e'ec+ec+ex+e'(e'+c'x') = = ec'+ec+ex+e' = e+e' = 1.
На все случаи жизни законами и правилами не запасёшься, поэтому гораздо лучше знать одну формулу импликации и на её основе проверять все спорные ситуации. Проиллюстрируем это утверждение весьма показательным примером.
Пример 2
Дана система логических уравнений[9]:
ax = bc, bx = ac.
Найти х.
Решение
Напрашивается простой и очевидный метод решения: сложить левые и правые части уравнений. В результате получим (a+b)x = (a+b)c. Откуда после сокращения на общий множитель имеем x = c, a = b. Ответ настораживает. Действительно, сложить левые и правые части уравнений мы можем на основании правила (9П) Порецкого. Кстати, заодно и проверим это правило:
(9П) (e=c) -> (e+b=c+b) = ec'+e'c+(e+b)(c+b)+(e+b)'(c+b)' =
= ec'+e'c+ec+b+e'b'c' = 1;
Да, Порецкий не ошибся. Однако относительно сокращения на общий множитель великий русский учёный нам ничего не сообщил. А так хочется это сделать, тем более что всё очевидно, и обычная алгебра нам не запрещает подобные операции. Проверим допустимость сокращения на общий множитель с помощью алгоритма "Импульс":
(cx=cy) -> (x=y) = cx(cy)'+(cx)'cy+xy+x'y' = cxy'+cx'y+xy+x'y' № 1.
Оказывается, что алгебра логики не разрешает нам этакие вольности. Решим поставленную задачу с помощью алгоритма "Селигер".
Алгоритм "Селигер" предполагает не только графическую, но и аналитическую минимизацию методом обобщённых кодов [6]. Для систем уравнений с числом аргументов не более 10 графический метод эффективнее. Минимизация в четырёхзначной комплементарной логике для двоичных аргументов несущественно отличается от минимизации в двузначной : нужно лишь проводить раздельное склеивание по i, j, 1 и 0.
По алгоритму "Селигер" :
M = (ax = bc)( bx = ac) M' = (ax Е bc) + ( bx Е ac) = ab'x+ac'x+a'bc+bcx'+a'bx+bc'x+acx'+ab'c.
После занесения M'в карту Карно получим
M = a'b'+abcx+c'x'.
Откуда решение системы логических уравнений в соответствии с алгоритмом "Селигер" примет вид:
x(a,b,c) = abc+ia'b'+jc(ab'+a'b); x(a,c) = ac+ia'. a(b,c,x) = bcx+ic'x'+jb(cx'+c'x); a(b,c) = bc+ic'.
Такой же результат можно получить, используя более наглядный,но и более трудоёмкий метод, представив уравнение для М в виде скалярных диаграмм.
a -------------------------======---- b -------------------------====----== c --------------=========------------ x ------========-----===-------------
Пример 3
В [1, стр. 378] приводится пример уравнения вида
M = ab+a'c.
Если умножить обе части этого равенства на a, то получим a = ab.
Умножив обе части на a', получим a' = a'c. Это результаты Порецкого. Проверим их по алгоритму "Селигер".
Табл. 5.
| abc | M | b | a | c | a | bc | a | |||
| 110 | 1 | 1 | 1 | 0 | 1 | 10 | 1 | |||
| 111 | 1 | 1 | 1 | 1 | 1 | 11 | 1 | |||
| 001 | 1 | 0 | 0 | 1 | 0 | 01 | 0 | |||
| 011 | 1 | 1 | 0 | 1 | 0 | 11 | 0 |
Из сводной таблицы истинности получаем следующие соотношения:
a(b) = ib; a(c) = c'+ic; a'(c) = ic; a(b,c) = bc'+ibc+jb'c'.
Из [4] известно, что
a(b) = ib = Aab; a(c) = c'+ic = Ac'a; a'(c) = ic = Aa'c;
Полученные уравнения изобразим в виде скалярных диаграмм[3]:
a ======------------------ b ===========---------- c ---===============
Скалярные диаграммы наглядно подтверждают правильность решения логических уравнений как по алгоритму "Селигер", так и по методу Порецкого.
Отыскание обратных функций
Используя алгоритм "Селигер" или "Селигер-С"[7
,8], можно получить полную систему обратных функций для двоичной логики. В таблице 6 приведена полная система функций двоичной логики.
Табл. 6
| xy | z0 | z1 | z2 | z3 | z4 | z5 | z6 | z7 | z8 | z9 | z10 | z11 | z12 | z13 | z14 | z15 |
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 01 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 10 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 11 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Перестановкой столбцов у и z исходной таблицы строим таблицу истинности для полной системы обратных функций.
Табл. 7
| xz | y0 | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | z11 | z12 | z13 | z14 | z15 |
| 00 | I | i | i | i | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | j | j | j | j |
| 01 | J | j | j | j | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | i | i | i | i |
| 10 | I | 0 | 1 | j | i | 0 | 1 | j | i | 0 | 1 | j | i | 0 | 1 | j |
| 11 | J | 1 | 0 | i | j | 1 | 0 | i | j | 1 | 0 | i | j | 1 | 0 | i |
Аналогичную таблицу можно было бы построить и для x = f0(y,z). Из таблицы обратных функций получаем полную симметричную систему обратных функций y = f1(x,z),а по алгоритму "Селигер" - y = f2(x), x = f3(y) :
у0 = iz'+jz y0 = j x0 = j у1 = xz+ix'z'+jx'z y1 = x+jx' x1 = 1 у2 = xz'+ix'z'+jx'z y2 = jx' x2 = y'+j у3 = i(xz+x'z')+j(xz'+x'z) y3 = ix+jx' x3 = 1 у4 = x'z+ixz'+jxz y4 = x'+jx x4 = jy' у5 = z y5 = 1 x5 = iy+jy' у6 = xz'+x'z y6 = x' x6 = y' у7 = x'z+ixz+jxz' y7 = x'+ix x7 = y'+iy у8 = x'z'+ixz'+jxz y8 = jx x8 = jy у9 = xz+x'z' y9 = x x9 = y у10 = z' y10 = 0 x10 = iy'+jy у11 = x'z'+ixz+jxz' y11 = ix x11 = y+iy' у12 = i(xz'+x'z)+j(xz+x'z') y12 = ix'+jx x12 = 0 у13 = xz+ix'z+jx'z' y13 = x+ix' - импликация x13 = iy у14 = xz'+ix'z+jx'z' y14 = ix' x14 = iy' у15 = iz+jz' y15 = i x15 = iy
Кстати, переход от левой системы уравнений к правой(от f1 к f2) легко выполняется простой заменой z на 1 и z' на 0. Аналогичные результаты мы получим, если таблицу прямых функций заменим скалярными диаграммами, а из них по алгоритму ТВАТ[3,8] выведем соотношения y = f(x). Самой примечательной из полученных функций является y13 = x+ix' - импликация. Из этого выражения легко просматривается физический смысл импликации: из истинности x следует истинность y.
Решая ту же самую задачу методом Порецкого,т.е. домножая в равенстве для М левую и правую части на x, x', y, y', мы получим следующие соотношения:
y0 - нет решения x0 - нет решения y1 = 1 x1 = 1 y2 = 0 x2 = 1 y3 = xy x3 = 1 y4 = 1 x4 = 0 y5 = 1 x5 = xy y6 = x'y x6 = xy' y7 = y+x' x7 = x+y' y8 = 0 x8 = 0 y9 = xy x9 = xy y10 = 0 x10 = xy' y11 = xy x11 = x+y y12 = x'y x12 = 0 y13 = x+y x13 = xy y14 = x'y x14 = xy' y15 = y x15 = x
Решая 1-ю задачу Порецкого[4], мы заметили аналогию между рекурсивным вхождением функции и комплементарным значением i. Резонно предположить, что такая аналогия существует между комплементарным j и рекурсивным значением инверсии функции. Проверим это предположение на полученных одноаргументных функциях и убедимся в их обратимости с помощью формулы эквивалентности. Заодно представим решение в скалярной форме.
0) (y = j) є (y = y')
M = (y=y') = yy'+y'y = 0
Нет графического представления.
1) (y = x+jx') є (y = x+x'y') = (y = x+y') x ============= M = (y=x+y') = y(x+y')+y'(x+y')' = xy+y'x'y = xy y ============= 2) y = jx' є x'y' x ============= M = (y=x'y') = yx'y'+y'(x'y')' = y'(x+y) = xy' y ---------------------- 3) y = ix+jx' є xy+x'y' x ============= M = (y=xy+x'y') = y(xy+x'y')+y'(xy'+x'y) = xy+xy' = x y ======------------ 4) y = x'+jx є x'+xy' = x'+y' x ---------------------- M = (y=x'+y') = y(x'+y')+y'(x'+y')' = x'y y ============= 5) y = 1 x =======----------- M = (y=1) = y&1+y'&0 = y y ============= 6) y = x' x ========-------- M = (y=x') = xy'+x'y y -------------===== 7) y = x'+ix є x'+xy = x'+y x ========-------- M = (y=x'+y) = y(x'+y)+y'(x'+y)' = y+xy' = x+y = Ax'y y --------======== 8) y = jx є xy' x ---------------------- M = (y=xy') = yxy'+y'(xy')' = x'y' y --------------------- 9) y = x x ======----------- M = (y=x) = x'y'+xy y ======----------- 10) y = 0 x =======---------- M = (y=0) = y&0+y'&1 = y' y ---------------------- 11) y = ix є xy x =======--------- M = (y=xy) = yxy+y'(xy)' = xy+y' = x+y' = Ayx y ====-------------- 12) y = ix'+jx є x'y+xy' x --------------------- M = (y=x'y+xy')=y(x'y+xy')+y'(x'y'+xy)=x'y+x'y' = x' y ====-------------- 13) y = x+ix' є x+x'y = x+y x ====--------------- M = (y=x+y) = y(x+y)+y'(x+y)' = y+x'y' = x'+y = Axy y ========-------- 14) y = ix' є x'y x =====------------- M = (y=x'y) = yx'y+y'(x'y)' = x'y+y' = x'+y' = Exy y -------------===== 15) y=i є y x =======---------- M = (y=y) = y&y+y'&y' = y+y' = 1 = Ixy(8) y ------=======----
После обращения были получены все 16 прямых функций от двух аргументов без какого-либо искажения. Это подтверждает правильность всех алгоритмов решения логических уравнений и корректность комплементарной логики. Если применить аналогичную процедуру к обратным функциям, полученным по методу Порецкого, то обратимость для М может быть обеспечена лишь при использовании сразу двух функций в виде логического произведения. Например, для y12 = x'y получим:
M = (y = x'y) = x'y+y'(x+y') = x'y+y' = x'+y',
что не соответствует исходному M = x'.
Однако, если мы используем обе обратные функции, то результат будет положительным:
M = (x=0)(y=x'y) = x'(x'y+y') = x'(x'+y') = x'.
Данное обстоятельство свидетельствует о том, что метод Порецкого не всегда даёт полное решение.
Заключение
Литература